Team Meeting（9.19）

Work Overview

Over the past two weeks, I have reviewed three research papers primarily focused on the path planning of large-scale Unmanned Aerial Vehicles (UAVs). In this section, I will deliver a comprehensive analysis of their conclusions.

1.Large scale aerial multi-robot coverage path planning

This paper was assigned to me during summer holiday and an overview was written.

Overview

In conclusion, this proposed multi-robot path planning method significantly enhances the efficiency of coverage over arbitrary areas of interest by leveraging the SPLIT and LINK TILES (SALT) strategy. By integrating this divide-and-conquer approach with our existing POPCORN framework, we not only reduce the computational time required for route planning but also enable scalable and parallel processing of multiple instances. This innovation allows for effective deployment of robotic networks in extensive environments, ultimately improving the accuracy and effectiveness of population counting and other coverage-related tasks. Future work will explore further optimizations and the practical implementation of this method in real-world scenarios, paving the way for more advanced robotic applications in various fields.

POPCORN

Our core algorithmic contribution, POPCORN, addresses a series of Boolean assignment problems within a Satisfiability Modulo Theories (SMT) framework. This approach offers significant advantages, as each problem can be solved considerably faster than a mixed integer linear program (MILP) of equivalent size. By efficiently producing paths that adhere to various constraints—such as maximum path length bounds and the requirement for cyclical paths—POPCORN demonstrates its effectiveness in optimizing multi-robot path planning. This not only enhances computational efficiency but also ensures that the generated paths are practical and feasible for real-world applications. As we continue to refine this methodology, we anticipate further improvements in both speed and scalability, ultimately leading to more robust solutions in the realm of robotic coverage and navigation.

POPCORN’s mathematical principles are primarily rooted in Boolean logic, combinatorial optimization, and constraint satisfaction theory. At its core, POPCORN transforms the path planning problem into a series of Boolean expressions composed of Boolean variables, which represent different states or conditions of the path, such as whether the path passes through specific points or meets certain constraints. This transformation allows the use of Boolean Satisfiability (SAT) solvers to determine if there exists a variable assignment that makes the entire expression true. Additionally, POPCORN operates within the framework of Satisfiability Modulo Theories (SMT), which extends SAT by incorporating more complex mathematical theories, such as integer and real number theories, allowing it to handle intricate constraints like path length limits and geometric properties. The path planning problem is viewed as a Constraint Satisfaction Problem (CSP), where multiple variables (path points) and constraints (length, shape, cyclical nature) are expressed as Boolean formulas. The goal is to minimize or maximize a specific function, such as minimizing path length or maximizing coverage area, and dynamic programming techniques may also be employed for optimizing path choices. By leveraging these mathematical foundations, POPCORN efficiently generates valid paths that meet the specified criteria, allowing real-time adjustments based on field conditions without needing to recalculate the entire route. This combination of Boolean logic, SMT theory, and optimization techniques makes POPCORN a robust tool for multi-robot path planning, particularly in applications like ecological monitoring and population counting.

Conclusion

The path planning component of the POPCORN algorithm is a systematic and efficient process designed to optimize coverage for robotic systems. It begins with a thorough analysis of the inputs, including the area of interest and coverage requirements. By overlaying a grid on the defined region, POPCORN ensures that path generation adheres to specified overlap and coverage criteria.

The algorithm employs various path planning strategies, such as zigzag and spiral patterns, to create optimized paths that minimize travel distance while satisfying constraints like maximum path length and cyclical requirements. Feasibility checks are conducted to confirm that paths avoid obstacles and no-fly zones.

The output consists of a series of waypoints that guide the drones, which are formatted into commands for the flight control system. Additionally, simulation and validation steps ensure that the planned paths meet coverage metrics, allowing for adjustments before deployment.

Finally, the flexibility of POPCORN enables real-time adjustments to paths in response to unforeseen obstacles, ensuring efficient and effective area coverage. Overall, POPCORN combines mathematical modeling, optimization techniques, and adaptability to facilitate successful robotic path planning in ecological monitoring and population counting applications.

SALT(Split and Link Tiles)

Since the aircraft cannot take off from any arbitrary position, the authors first list several takeoff points (referred to as “homes” in the text) and require that the aircraft taking off from a specific home must return to its corresponding home after completing its mission. Each path $p_k$ can be described by a starting position $H_k \in H$ and a set of nodes $V_k$:

$$p_k = (H_k, V_k = \{v^k_1, ..., v^k_n\}) \text{ where } v^k_i \in V \text{ and } (v^k_i, v^k_{i+1}) \in E$$

Next, due to the constraints of flight efficiency and battery capacity, the authors consider maximizing the reduction of flight time. Therefore, they adopt a closed-loop flight path, meaning that the endpoint of the reconnaissance path is the same as the starting reconnaissance position of the aircraft, mathematically expressed as $v_1^k = v_n^k$, as illustrated in the figure below:

The closed-loop path diagram, where the light blue indicates the starting and ending points of the aircraft's reconnaissance.

The length $s_k$ of each path $p_k$ can be described as:

$$s_k = \sum_{i=1}^{n} \|L(v_{i+1}) - L(v_i)\|$$

where $n$ is the number of nodes on the path $p_k$ and $L(v_i)$ denotes the coordinate position of node $v_i$.

Since these paths form a loop, we can shift the index of the reconnaissance path and “attach” the home point:

$$h_k = \arg\min_{H_k \in H} \min_{v \in V_k} \|H_k - L(v)\|$$

Now, we can provide the overall flight time formula as:

$$t_k = 2 \frac{h_k}{v_h} + \frac{s_k}{v_s} \leq T_{\max}$$

where $\frac{h_k}{v_h}$ is the time the aircraft takes to travel from the takeoff point to the reconnaissance point, and $\frac{s_k}{v_s}$ represents the time spent by the aircraft during reconnaissance, which must be less than the aircraft’s maximum endurance time.

Finally, the overall model is given as:

$$\begin{align*} \min \sum_{k=1}^{K} t_k \\ \text{s.t.} \quad t_k &< T_{\max} \\ \bigcup_{k=1}^{K} V_k &= V \end{align*}$$

If we also want to consider achieving the most economical situation, we need to take into account reducing the number of aircraft takeoffs. In this case, the model can be described as:

$$\begin{align*} \min \ K \\ \text{s.t.} \quad t_k &< T_{\max} \\ \bigcup_{k=1}^{K} V_k &= V \end{align*}$$

where $K$ is the number of flights of the aircraft.

2.Large-Scale Multi-Robot Coverage Path Planning via Local Search

Overview

The graph-based Multi-Robot Coverage Path Planning (MCPP) studied in this paper introduces a new approach through the LS-MCPP framework to address the problem of multiple robots covering all vertices of a given 2D grid terrain graph $𝐺$. Unlike existing algorithms, LS-MCPP systematically searches for effective coverage paths directly on the decomposed graph $𝐷$, optimizing the generation of coverage paths. By introducing the Extended Spanning Tree Coverage (ESTC) paradigm, the paper achieves complete coverage for MCPP on any decomposed graphs, even when dealing with incomplete terrain graphs.

Extended-Spanning Tree Coverage(ESTC)

Mathematical Principles of the Extended Spanning Tree Coverage (ESTC) Paradigm

This section explains the Extended Spanning Tree Coverage (ESTC) paradigm, which addresses coverage problems on incomplete terrain graphs and extends its application to multi-robot coverage path planning (MCPP).

1. Definition of Terrain Graph

• Given a terrain graph $ G $, each vertex $\delta_v$ can be decomposed into four vertices. A vertex is defined as “complete” if all four decomposed vertices are present in the decomposed vertex set $V_d$; otherwise, it is “incomplete.”
• A terrain graph is “complete” if all its vertices are complete; otherwise, it is “incomplete.”

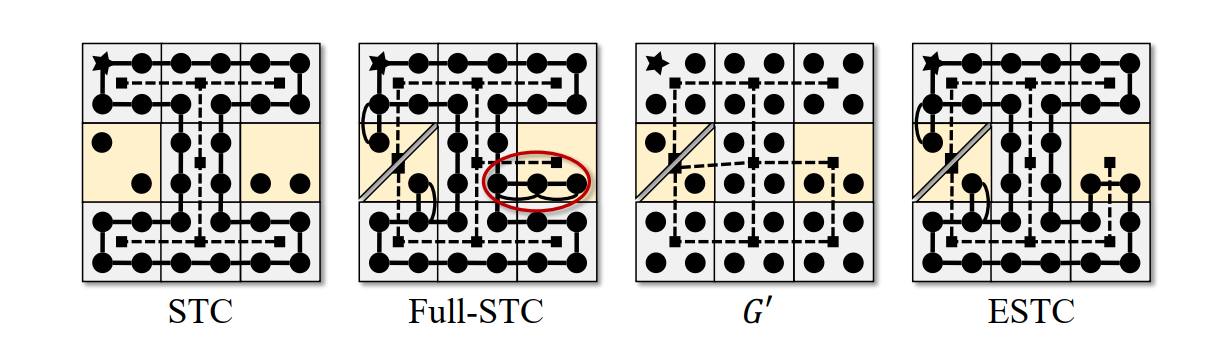
2. Limitations of STC Algorithm

• The standard Spanning Tree Coverage (STC) algorithm only works on complete terrain graphs because it relies on traversing spanning edges in the graph $G$.
• For incomplete graphs, STC fails to find optimal solutions, especially because certain incomplete vertices may not be reachable through standard path traversal.

3. Design of ESTC

• ESTC addresses the coverage of incomplete terrain graphs by integrating the path-deformation technique from Full-STC into its offline computation. Full-STC is designed for online single-robot coverage on unknown terrain but is suboptimal for known graphs because it doesn’t account for different path costs from spanning trees.

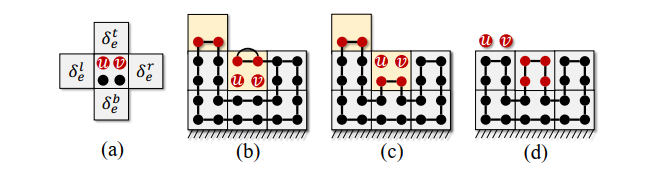
• In ESTC, an augmented terrain graph $G'$ is created by removing certain edges to reflect connectivity between vertices. For example, if a terrain vertex has only two diagonally opposite decomposed vertices, it is replaced by two non-adjacent vertices in $G'$.

• ESTC introduces non-uniform edge weights to prioritize using edges connecting complete vertices. For edges connecting incomplete vertices, the edge weight is manipulated by the following formula:

  $$w(\epsilon) = w_{\max} \cdot \frac{1}{2} \cdot \left( \sum_{\epsilon \sim \delta_u} w_{\epsilon} + \sum_{\epsilon \sim \delta_v} w_{\epsilon} \right)$$

  This formula ensures priority for edges connected to complete vertices and reduces unnecessary coverage of incomplete vertices due to rerouting.

4. Building the Minimum Spanning Tree (MST)

• ESTC constructs a minimum spanning tree (MST) on the augmented graph $G'$. The algorithm follows a path-deformation rule, ensuring that the robot reroutes to the left side of a spanning edge if the right side is blocked due to non-adjacency between decomposed vertices.
• The manipulated edge weight from the previous formula prioritizes making incomplete vertices leaves of the MST, improving coverage efficiency by minimizing repeated coverage.

5. Extension to MCPP (Multi-Robot Coverage Path Planning)

• ESTC is extended to multi-robot coverage path planning (MCPP). For a multi-robot instance $(G, D, R)$, each robot is assigned a subgraph $D_i$, which could be incomplete.
• ESTC is applied to each subgraph by constructing a minimum spanning tree on the augmented graph and generating the coverage path, ensuring that all robots jointly cover the entire terrain graph $D$.

6. Sufficient Condition for Complete Coverage

• Theorem 1 states that if each subgraph $D_i$ is connected and the union of all subgraphs’ vertex sets equals $V_d$, then ESTC guarantees complete coverage of the entire terrain graph.

---

Key Ideas

• Path Deformation and Edge Weight Prioritization: ESTC avoids redundant coverage by deforming the path when necessary and using weighted edges to prioritize connections between complete vertices.
• Use of Minimum Spanning Tree: By constructing the MST on an augmented terrain graph, ESTC generates optimized coverage paths, even on incomplete graphs.
  

---

Boundary Editing Operators

Overview

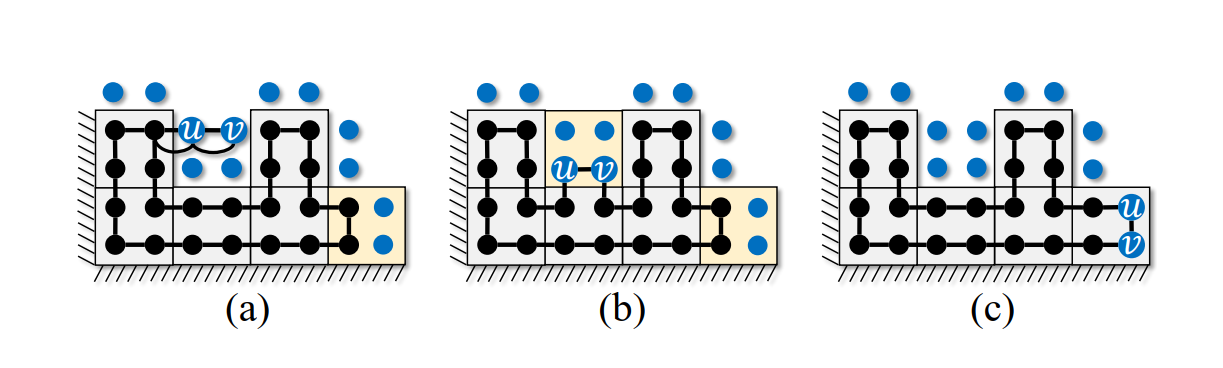
Boundary editing operators are methods used to modify subgraph boundaries by adding or removing vertices. These operators aim to optimize coverage while maintaining connectivity and ensuring complete coverage of all vertices.

Definitions

• Duplicate Set $V^+$: A set of vertices covered by multiple subgraphs, calculated as:

  $$V^+ = \{v \in V_d \mid n_v > 1\}$$

  where $n_v$ is the occurrence count of vertex $v$ across all subgraphs.

• Edge Set $F_i$: Edges within a subgraph $D_i$ with endpoints derived from the same terrain vertex.

Operators

1. Growth Operator:
   • Expands a subgraph to include additional vertices adjacent to it.
   • Adds edges $e = (u, v)$ and related connecting edges to $D_i$ if parallel edges $(p, q)$ exist in $D_i$.
   • Adds $u, v$ to $V^+$ if they are covered by other subgraphs.

2. Deduplication Operator:

   • Removes unnecessary duplicates from a subgraph.
   • Removes edge $e = (u, v)$ if $u, v \in V^+ \cap V_{d,i}$ while maintaining connectivity.
   • Conditions depend on whether $\delta_u$ is complete or incomplete.
     

3. Exchange Operator:

   • Combines growth and deduplication to efficiently manage duplicates.
   • Transfers edges between subgraphs while ensuring conditions for growth and deduplication are met.
   • $V^+$ remains unchanged.

Properties

• Subgraphs remain connected after any operation.
• The union of all subgraph vertex sets always equals the original vertex set $V_d$.

These operators are designed to improve solutions for multi-robot coverage path planning (MCPP) and ensure efficient edge-based terrain coverage (ESTC).

LS-MCPP

The LS-MCPP algorithm takes an initial solution for a Multi-Robot Coverage Path Planning (MCPP) problem and iteratively improves it using a search-based approach inspired by simulated annealing. It begins by initializing pools of operators (grow, deduplicate, exchange) and a temperature scalar $t$ to control acceptance of non-improving solutions. A pool weight vector $p$ is used with a softmax function for probabilistic selection of operators from these pools.

For each iteration, the algorithm samples an operator based on a heuristic function, applies the operator to modify the solution, and evaluates its effect on the makespan. Solutions with reduced makespan are accepted immediately, while non-improving ones are accepted based on a probability controlled by $t$ and the makespan increment, following a simulated annealing strategy. Over time, $t$ decays, making it harder to accept non-improving solutions, thus guiding the search towards a local or global optimum.

At regular intervals, or when the best solution so far is found, the FORCEDDEDUPLICATION() function is invoked to improve the solution further. The process continues until either a maximum number of iterations is reached or no further improvements can be found. The algorithm then returns the best-found solution $Π∗$.

Future Plan

1. Reading Papers Consecutively

I choose a few more papers related to the Multiple-Robot Coverage Path planning(MCPP) topic to read which can help me to have a deeper understanding on this topic. There are the papers that i am going to read:

1. Collins, L.; Ghassemi, P.; Esfahani, E. T.; Doermann, D.; Dantu, K.; and Chowdhury, S. 2021. Scalable coverage path planning of multi-robot teams for monitoring non-convex areas. In IEEE International Conference on Robotics and Automation (ICRA), 7393–7399.
2. Song, H.; Yu, J.; Qiu, J.; Sun, Z.; Lang, K.; Luo, Q.; Shen, Y.; and Wang, Y. 2022. Multi-UAV disaster environment coverage planning with limited-endurance. In International Conference on Robotics and Automation (ICRA), 10760–10766.
3. Zheng, X.; and Koenig, S. 2007. Robot coverage of terrain with non-uniform traversability. In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 3757–3764.
4. Li, L.; Shi, D.; Jin, S.; Yang, S.; Lian, Y.; and Liu, H. 2023. SP2E: Online spiral coverage with proactive prevention extremum for unknown environments. Journal of Intelligent & Robotic Systems, 108(2): 30.
5. Westheider, J., Rückin, J., & Popović, M. (2023, October). Multi-uav adaptive path planning using deep reinforcement learning. In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 649-656). IEEE.

Reference

【1】Shah, K., Schmidt, A., Ballard, G., & Schwager, M. (2022). Large scale aerial multi-robot coverage path planning. Field Robotics, 2(1).
【2】Tang, J., & Ma, H. (2024, March). Large-Scale Multi-Robot Coverage Path Planning via Local Search. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 38, No. 16, pp. 17567-17574).